Chapter eight
Standing Waves in Photoreceptors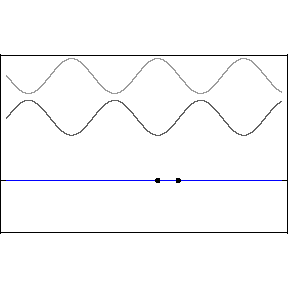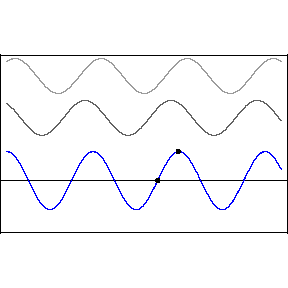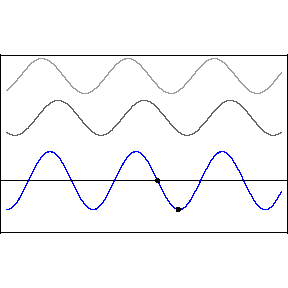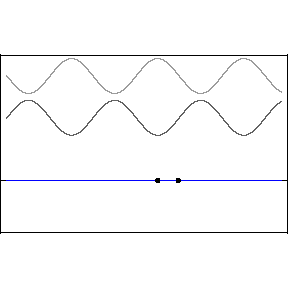

Animation courtesy of Dr. Dan Russell, The Pennsylvania State University.

One cannot, ruler in hand, race alongside a light wave in hopes of measuring its wavelength or its phase relative to an adjacent light wave. The great appeal of standing waves is precisely that they are standing still, and therefore susceptible to sensing and measurement, specifically at the backwall of the eye. In the animation, the blue wave pumps up and down but remains stationary on the x-axis — hence the name, “standing” wave.

Let’s start with a quick review of how standing waves form. The two upper light waves are identical, moving at lightspeed in opposite directions. They are separated here for clarity but one should imagine both waves moving in opposite directions along the same axis.

This pattern would occur if an incoming wave (let’s say the uppermost, rightbound wave) encountered a mirror and was reflected back along its original path. The reflected wave is represented in the animation as the middle wave. The bottom wave, that is, the blue standing wave, results from the superposition and algebraic addition of the upper two.

A measurement or detection of the peak-to-peak distance of the stationary wave would tell us the wavelength of the incoming light, that is to say, its color.

As one mentally accelerates these ultraslow motion depictions of waves, the standing wave acquires the fixed-in-place appearance of beads on a string.
Because the wave is sitting still, it is easy to take measurements from it. If these were radio waves, for example in the amateur 2-meter band, one could simply walk along the radiation pattern with a handheld sensor and detect the succession of peaks and nulls (antinodes and nodes). Various electronic frequency measuring instruments are based on the principle of standing wave detection and measurement.

For visible light, however, the wavelength is much shorter, on the order of 400 nanometers to 700 nanometers.

It is extraordinary – a triumph, actually — to capture an image of a standing wave at this tiny dimensional level. Conventional optical microscopy is not helpful. This is because the microscope’s optical resolution approaches its ultimate limit, which is half the wavelength of the very lightwave we would wish to observe.

It is possible to break past this conventional resolution limit, however, using the novel technique of scanning near field optical microscopy (SNOM). Solid state physicists working with W1 photonic crystal waveguides have made standing waves in this regime a focus of study. One remarkable result is the standing wave image reproduced below. The work is described in detail in a 2005 paper in Applied Physics Letters by Robert Wüest et al at ETH in Zurich.

Dr. Wüest kindly contributed the following description of the image he obtained using scanning near field microscopy. This is a
standing wave produced in a photonic crystal waveguide using a laser source at wavelengths ranging from 1480 nm to 1495 nm:


In scanning near-field optical microscopy (SNOM) a subwavelength fiber tip is used to pick up the light at the surface of a structure. The tip is scanned at a constant height of 10-20nm above the surface and thus, the topography and the optical-field information is acquired simultaneously with a resolution of roughly 100nm. This method was used to characterize photonic crystal based integrated optics waveguides at telecom wavelengths. The SNOM images show the standing wave inside of a terminated W1 waveguide, in a very intuitive and at the same time quantitatively accurate way. Such measurements were used to characterize the photonic crystal waveguides concerning their dispersion relation and the propagation loss with a high degree of accuracy.

Incidentally, the SNOM technique has been applied with interesting results in scrutinizing neurons. Here is a report in a book on nano-optics. It takes a bit of navigating. Click the “Search Books” button at the very top of the page, and then click the search results for page 183. Several other pages are accessible on line that discuss scanning biological material. Also, here is a paper that may be helpful as an entry point.

Standing waves in the eye?
The physiologist W. Zenker first remarked on the possibilities for color sensing based on the detection of standing waves in retinal photoreceptors in 1867. (Zenker, W. Versuch einer Theorie der Farbrezeption, Arch. F. mikrosk. Anatomie 3, 248 ff, 1867). The idea has persisted ever since, in a sort of shadow literature on color detection in the eye. Zenker never sensed a conflict between trichromacy and his own standing wave theories. But after Zenker the literature becomes divergent in the sense that it explores ideas which are, for the most part, politically positioned by their authors as conflicting with, or even as revolutionary alternatives to, the almost universally accepted Young-Helmholtz or trichromacy model of color detection.

I am not sure that the two models could not be rather easily reconciled or in some way quite logically enfolded into each other but, in any event, the standing wave color theorists typically present their ideas as alternatives to trichromacy. The early papers are in German and the most recent papers are in English, but the locus of interest in these ideas, and the research that has devolved from them, seems to be centered in northern Europe, in Germany and Denmark.
3D illustrations of rod and cone cells courtesy of Dr. Roger C. Wagner, Professor of Biology, University of Delaware.

One idea is that a cone or rod can be modeled as a dimensionally tuned cavity, resonant at a specific color wavelength. This is a second cousin of the trichromatic model, in that each photoreceptor is wavelength specific. But instead of just three major cone types, each with a maximum sensitivity set for one of three different colors, the resonant cavity hypothesis offers a much wider variety of dimensionally diverse photoreceptors, each attuned to a different specific color.

The charming quality of tuned cavity color vision is its shared physics with tuned musical instruments. In this particular standing wave hypothesis, the retina is analogous a cathedral organ. Lots of pipes of different diameters and lengths. When you try to visualize how this pipe organ metaphor might apply in practice, in the eye, it turns into a real puzzler — but the basic resonant cavity idea seems solid nevertheless.

 

The tuned dimensions of a rod or cone are diameter and length. (Incidentally foveal cones, which is to say, most cones, do not actually taper. They are cylindrical rather than conical. There is subtantial statistical variation across the retina in cone diameters and lengths.) To get a sense of how sensitive standing waves can be to dimensional parameters, click to this string animation. Hit the start button, slide to wavelength multiples of 25, i.e., 25, 50, 75, 100 and 125 and watch the resonance effects.

The self-tuning trombone
In a slightly more mechanized and, in my opinion, more readily workable standing wave photoreceptor hypothesis, physically, the resonant cavity is seen as self-tuning, so that each photoreceptor can respond across a spectrum of color.

It was first observed in 1943 (by Detwiler) that retinal rods elongate and contract in light and darkness, respectively. The effect was studied carefully in the 60s and 70s, and it was shown by Wolken that in vitro, a severed rod outer segment can actually double in length when illuminated — without a change in diameter. In darkness, if ATP is added back, the outer segment contracts, returning to its normal length. These are not passive changes. Photoreceptors are descended of cilia. They contain contractile and structural proteins that enable active mechanical changes and movement

In life and in theory and in daylight, the length changes in the outer segment need not be so extreme.

If the outer segment is viewed as a dimensionally tuned resonator for standing waves, then tiny incremental changes in cylinder length could bring the rod into resonance with an incoming light wave — thus maximizing the intensity of the standing wave. The proposed self-tuning effect works like sliding a trombone — or simply nudging the slider in this animation. Hit the Start button, turn on the ruler, and try values approaching and at 100 MHz.

To make the tuning process automatic in the eye, i.e., self-tuning, requires a feedback loop. Or the receptor could simply oscillate in length a bit, continually scanning for, and passing through, resonances.

Another hypothetical self-tuning mechanism, sort of a calmer, more sophisticated, solid state alternative, does not require any mechanical movement. In this concept self-tuning results from the alteration, by incoming light, of the transmittance/reflectance property of each disk. This is a chemical change which is accompanied by changes in optical properties and dimensions. It was originally characterized as “bleaching.” It can be modeled as the positioning or re-positioning — at wavelength intervals — of multiple mirrors.

One receptor, all colors
In the most optimistic view of these self-tuning models, each photoreceptor can report the reception of any color. From a purely engineering standpoint — setting aside for the moment questions of spectral range and of biological plausibilty — this is a very appealing approach.

In the eye, each photoreceptor is a point of convergence. When light hits a point on an object in the world, it scatters in all directions. The lens of the eye differentially refracts some of the rays originating from that specific point in space and focuses them back into a single spot on the retina – a photoreceptor.

Thus, each photorecepter positioned in the image plane of the lens responds, electronically, to a specifc point in the world. It would be ideal if the brain could somehow directly and instantly read, at each photoreceptor, the color of the light arriving from the conjugate point on the object we happen to be looking at. The payoff would be the best possible resolution that can be obtained from a given population of photoreceptors.

 

In the textbook trichromacy model, cones are “color blind,” in that they respond to many different light wavelengths across a spectrum centered on an absorption peak. Mentally pull a horizonal line across this graph at a y-axis value of 50, and regard it as an intensity reading from a red cone. Notice where the line would intersect the red absorption curve. A red cone intensity readout of 50 could mean the impinging light has a wavelength of 500 nm, which is blue-green — or it could mean with equal authority that the impinging light has a wavelength of 625 nm, which is red. The intensity reading from a cone is perfectly ambiguous.

Therefore a comparision of the intensity output of one cone with that of another cone — one with a different absorption peak — is absolutely required to produce a meaningful determination of color. A specific color wavelength is not directly measured by any single cone. It must be deduced.

Thus, in the trichomatic model it takes at least two photoreceptive cones, not just one, to sense the color of incoming light. It also takes additional circuitry to perform the logical evaluation of cones’ output signals.

The self-tuning standing wave models are much simpler. Each single cell can directly identify many colors — and the detector works across a whole spectrum of wavelengths. No output comparison or additional processing steps are required. A photoreceptor simply looks at a color and reports it.

However, when we say “a whole spectrum of wavelengths,” we should also say, to be realistic, something like “within a spectrum constrained by the wavelength range which is possible for that particular photoreceptor.” For example, a red cone could report any received wavelength within its range — a range defined and constrained by that cone’s photosensitive pigment. Each type of cone, Low, Medium and High wavelength, would cover an appropriate segment of the total spectrum.

In this view, the evolutionary point of using different photopigments is simply to extend the wavelength range of the eye. Within each of the three (or four) bracketed ranges, the specific wavelength of the incoming light, whatever it is, can be precisely sensed and reported using standing wave detection. The total responsive range is the same as that for the conventional model.

In the following paragraphs we will consider how a standing wave detector might work, briefly glance at two more standing wave models, and then circle back to look at the main historical objection to any and all of these standing wave photoreceptor hypotheses — supposedly their Achilles’ heel.

The detection system
The length of the outer segment of the retinal rod is usually taken to be about 25 microns, or 25,000 nanometers. If one were to align within the cylinder of the outer segment of a rod cell an incoming blue-green light wave of 500 nm wavelength, then the cylinder would encapsulate as many as 50 cycles. Rod outer segments may reach 45 nm in length, and cone outer segments can be over 50 nm long. And in rods, as in the trombone model, the cylinder length might actively vary from moment to moment. So for our purposes, let’s just say the outer segment of a photoreceptor could encapsulate 50 to 100 cycles of a standing light wave.

 

 

3D illustrations of rod and cone cells courtesy of Dr. Roger C. Wagner, Professor of Biology, University of Delaware.

The photosensitive disks wrapped like cookies in the outer segment are positioned at center-to-center intervals of 30 nanometers. Each disk is 15 nm thick. Each inter-disk space is also 15 nm. (In older literature you will find numbers like 20 nm center-to-center and a 10 nm disk thickness, but the 30 nm center-to-center and 15 nm thickness reflect the current view.)

Resolution of the sensor
Suppose we regard the disks as increments inscribed along a transparent ruler. To measure wavelength one might mentally overlay, on a standing wave cycle with a wavelength of, say, 500 nm, about 17 photosensitive disks upon each standing wave cycle, or “bead of light” appearing within the rod cylinder.
.
The 30-nanometer center-to-center interdisk interval is common to most photoreceptors and is often characterized in the literature as “almost crystalline” in its periodicity. Here are 17 disks viewed edgewise in a photomicrograph of the outer segment of a rod cell. The 30 nm “center to center” distance between disks implies a distance measured between idealized, one dimensional geometric detector planes. In fact the disks are rather meaty objects, 15 nm thick. Of this thickness the two closely stacked photoresponsive membranes of each disk have a combined thickness of perhaps 12-13 nn. The two membranes are so close together they appear as one thick line in this photomicrograph. Separating the two membranes there is just a 1.5-2.5 nm aqueous gap — a gap barely visible in this picture, except as a white dot near the disks’ rims.

Bear in mind that the rod structure depicted in the EM is dead as a doornail. In life, these membranes are surely a little plumper and juicier. This doubled-up membrane thickness necessarily fuzzes the resolution of the disk – it is not a perfect, one dimensional sensor plane. In other words we have a been handed a ruler on which each single increment is drawn-in as a closely spaced double line every 30 nm. Yet the rod’s resolution is still pretty impressive. As an approximation, I have superimposed the photomicrograph on a single bead of light. As noted, in the example of a 500 nm blue-green light wave, the rod cell positions 17 photosensitive disks, or increments, in each bead of light. The resolution is comparable and perhaps superior to the resolution of the SNOM device used to take the photo of the standing wave.

How to build a detector:
How can we make a color detector out of this? A simple model works like calipers. Suppose we wish to measure – on this string of beads of light — the peak-to-peak distances. The photoreceptive disks are each responding, as a function of light intensity, at finely graded (30 nm) increments along the Z-axis of the rod cell. Along the standing wave, some disks will register bright light — some disks will register light levels near darkness.By observing any two light intensity maxima (antinodes) of the standing wave, and then remarking the distance between these two peaks, we can call out a number which varies with the color of the incoming light. It would work equally well, in theory, to pick out a pair of light intensity minima, and jot down a number representing the distance between these two nodes. One could also measure the peak-to-node distance. So there are three ways to detect color using photoreceptive disks as though they were electronic calipers.

One could also simply count-up to or accumulate a signal proportional to beads per micron, or peaks per micron, or nodes per micron, since any such ratio would vary as a function of the incoming light’s wavelength. This approach has the advantages of averaging — it is a little less dependent on exact dimensions.

Intensity is amplitude squared, so the negative going excursions disappear. We know the nervous system typically triggers at preset thresholds of sensitivity. A threshold detector associated with each disk or, in the vernacular of analog electronics, a “peak picker”, could be set up to identify, that is, selectively trigger off of — light intensity peaks.

 

 

There are several other interesting hypothetical standing wave mechanisms. One imputes to the system reading the disks a pattern recognition ability, able to notice multiple harmonics and complex intensity patterns associated with mixed frequency inputs. This theory takes into account the fact of partial reflection.

Another hypothesis is based on the detection, at the disks, of distinct waveguide modes — unique geometric patterns that change rather abruptly as a function of wavelength. We will come back to this one.

The insurmountable 1-channel output problem.
In this review I have been using terms like “jot down” or “call out” or “count up” in order to avoid, up to this point, the tricky problem of how to export wavelength information from a photoreceptor as a nerve signal. Over the past 157 years, the standing wave hypotheses of color perception have all hit the wall on this problem.

A lot of interesting physics can happen when light hits a rod or cone, no question about it — but news of these intricate events is restricted to what can be transmitted via the rod or cone cell’s 1-channel output line.

Consider for example the cone cell. In the trichromacy theory, the cone cell is basically just a light meter. For a given center wavelength (one of three) the cone will produce a voltage output proportional to light intensity. The output signal will fade on either side of the absorption peak, and in this sense one could say that the voltage output varies with the input wavelength. But the point is, the textbook cone has no separate and distinct output signal that varies with light wavelength. There exists only one information channel out of the cone, and the cone uses it to signal its perception of light intensity — nothing more.

Reporting to the brain both intensity and wavelength (color), separately and simultaneously, could be accomplished pretty easily with a multichannel neuron. But given the 1-channel output, the standing wave theorists have been obliged to invoke some sort of yet-to-be-discovered serial signalling or other time-multiplexing scheme — in order to transfer wavelength information out of the photoreceptors.

This is probably why these theories have not, to date, gained much traction. Several of the proposed standing wave detectors make a lot of sense — as detectors, viewed in isolation — but there is no very direct way to plug them into the nervous system.

The photoreceptor, bipolar, amacrine and horizontal cells are analog type processors, so it is possible within the retina to communicate and process graded analog signals rather than action potentials. But as one tries to shift information from the eye toward the brain the problems become even more daunting, because the output lines – the retinal ganglion cells, the optic nerve – transmit all-or-none spikes. Now we are plunged into the familiar connundrum, and hopeless bottleneck, of neural encoding and decoding.

The idea that standing waves probably exist in photoreceptors is reasonable enough and is not strongly contested. Published mathematical models of photoreceptors commonly take into account both longitudinal and transverse standing waves. But the brain is believed to be completely oblivious to these standing waves.

In short, the concept of standing wave detection in photoreceptors has been brushed aside, historically, repeatedly, because in order to come up with a physiologically workable scheme in which the retina detects standing waves — one is almost obliged to reinvent the nervous system.

It is of course the premise of this book that — exactly, yes — the nervous system should indeed be reinvented, and that a multichannel neuron exists. We take it as a given, as the basis of our thought experiment. So within the logical framework of this book, we have a degree of freedom that was not available to the original standing wave theorists, and we hope to see what can be done with it.