Chapter three
Impulses that travel
without action potentials

Simplified, animated ion channel adopted from the University of Washington site. When the interior charge of the cell shifts in a positive direction (i.e., goes less negative) the positively charged voltage sensor rises. As the voltage sensor ascends it opens up a pore through the cell membrane. Depending on the type of ion channel, cations may enter or exit the cell via this open passage. This chapter explores the idea that a long line of linked voltage sensors could support the passage of an impulse in any neurite, not just the axon. The sensors are driven by a change in transmembrane voltage. The moving impulse could be powered by an action potential or by any of several alternative power supplies.

The multichannel neuron model developed in Chapter 2 depends upon the linkage of adjacent sodium channels. At this point in the story, the model applies only to unmyelinated axons that communicate using action potentials. But this is a special case. Perhaps we could broaden the hypothetical model to include all types of communication in all types of neurites, including dendrites.

It will prove helpful to ask this question: What specific part of a unit ion channel is to be functionally linked, in the model, to the next unit ion channel in line?

An ion channel has two components: the pore and the propulsive element – the voltage sensor. If we choose to functionally link the voltage sensors, using a successive unlatching mechanism, we may then be able to broaden the model to explain and include, in a completely general way, all types of informational nerve conduction.

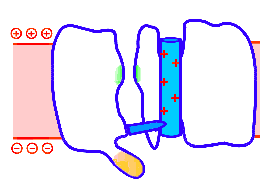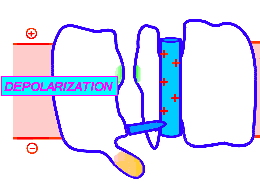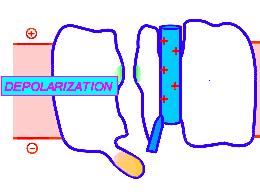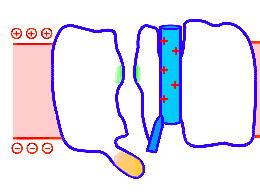
Looped animation showing a nerve “impulse” moving along a line of linked voltage sensors. Tops are slotted to demonstrate that the sensors both translate and rotate. To keep things simple, the animation shows a single voltage sensor per ion channel — in life there are four per channel. Voltage sensors are protein domains. In biochemical terms we can think of their activity in this animation as a wavefront of conformational change shifting from sensor to sensor. The links are hypothetical and are not shown, but their effect is clear: Via a link, each sensor unlatchs the next, so the wave moves as in a row of falling dominos. The upward propulsive force on all these voltage sensors, which are positively charged, is supplied by an underlying positive charge in the interior of the neuron.

This broader model of a nerve impulse includes not only action potentials but also silent, unsuspected nerve impulses that can move without accompanying action potentials: One can surmise that these “silent” impulses communicate in dendrites, in the outer segments of photoreceptor cells, in the internodes of myelinated nerves, and in the ultrafine neurons of C. elegans.

The unifying hypothesis is that all neurites communicate with impulses. These impulses, including action potentials, are conveyed by and along lines – wires, essentially – composed of a series of voltage sensors that are functionally linked by protein moieties. It will turn out this hypothetical linkage acts to latch and restrain the movement of each voltage sensor until the immediately preceding voltage sensor has shifted.

It is conceivable that a successive unlatching mechanism releases voltage sensors within the arrayed quad of sensors that opens a single ion channel — as well as triggering off the sensors in the next neighbor ion channel.

In this model, certain measurable potentials like the EPSP are power supplies. A sufficiently strong inhibitory potential can extinguish the flow of information.

Why tinker with success?
In the model sketched here, the advancing wavefront of a nerve impulse is carried by protein links between voltage sensors. In the textbook description of an action potential, the advancing wave front is carried by the leading edge of an expanding positive charge pool injected into the neuron by incoming Na+ ions. To see why this changeover in wave front carriers is necessary, let’s quickly review the qualitative implications of the standard model. It was originally worked out by Hodgkin, Huxley and Katz in 1952.

Visualize for the purposes of explanation an idealized axon with rings of unit sodium channels stacked in an orderly way all along its length. At the site of an initial ring of sodium channels surrounding the axon, an incoming positive charge is sensed by voltage sensors. The sensors move like pistons and in the process open up a ring of sodium pores. The ring of pores admits more Na+, and thus shifts the wave front of strong positivity one increment along the length of the axon — to the next ring of sodium channels.

Now new voltage sensors are in range, “feel” the new positive charge injected by the sodium ions, and react by opening new pores, admitting fresh sodium ions. By means of this stepwise and repetitive process the nerve impulse walks the length of an axon. Here is an animation — notice the green arrows showing influx of Na+ ions. The voltage sensors are hidden but you can see their work: Yellow, disk-shaped lids of ion channels pop open like hatch covers.

There is nothing objectionable about this automatic process, in which the longwise expansion of a positive charge inside the axon carries with it the nerve impulse’s wave front. However, it is a design that assumes a classical one-channel, all or none axon.

The single expanding wave front of positivity necessarily triggers off all unit sodium channels. There is no way in which this completely unselective, amorphous system could conserve the identities of individual, numbered longitudinal channels.

This is why, in the multichannel neuron model, it is necessary to propose a successive unlatching or “cock and fire” process that can be confined to and used by each of 300 individual longitudinal channels. This is simply a requirement of the multichannel model — the preservation of numbered channels — but by good luck it substantially simplifies the nervous system.

Incidentally, on an unmyelinated axon, the linked sodium channels that make up the multiple numbered longitudinal channels could be a subset of the total sodium channel population. Once the links between voltage sensors are put in place multichannel communication is assured in the model neuron. One could then pepper the membrane with unlinked unit channels. This would produce a more robust transmembrane power supply, in the manner of the HHK model.

Multichannel communication would be unaffected by unlinked sodium ports opening nearby because only the linked channels lead to synapses. The isolated, unlinked Na+ channels admit additional sodium and produce a textbook wave of depolarization that accompanies the real signal — but leads nowhere.

In other words isolated unit channels could provide an enhanced power supply. They would thus have only a supporting role to play in conveying a signal — a number — to the next neuron. However the unlinked channels would, in an instrumented experimental preparation, make the multichannel neuron “look like” the one-channel neuron depicted by the HHK model. And make it difficult to spot the real signal carried by linked Na+ channels.

This helps us meet both requirements for the model as stipulated at the beginning of Chapter 2: “To arrive at a fresh model of the neuron, it is necessary to stay within two rules. 1) because it is so slow, the impulse must carry a heavy load of information and 2) whatever the trick, the secret variable, it must elude detection by all the instruments commonly used to study nerves.”

Conduction as a hodgepodge
Textbooks typically recognize and discuss at least three types of nerve conduction: passive conduction in dendrites, conduction by action potentials in axons, and saltatory conduction in myelinated axons.

The story gets more complicated as you thread your way into it.

Many neurites communicate without action potentials. This type of signaling is thought to work in different ways in different components and nervous systems. In dendrites, communication is supposed to be driven by the algebraic summation of incoming excitatory and inhibitory potentials, although there are also rare dendritic spikes, or action potentials, in dendrites. In myelinated nerves, communication depends on apparent jumps from node to node — saltatory conduction. Action potentials drive this process, but they appear only at the nodes.

The nematode C. elegans has no voltage-gated sodium channels whatsoever. In certain C. elegans neurons that have been studied, transmembrane potential shifts up and down as though the whole (tiny) neuron were analogous to a bistable multivibrator circuit.

In photoreceptors, whose outer segments are nominally dendrites, the mode of communication is reported to be analog – but there are reports of action potentials in photoreceptors as well.

Net, nerve conduction is not understood as a single phenomenon. It is a hodgepodge of different phenomena and modes. This means that in the textbook nervous system, there must be frequent transitions between one mode of conduction and another. These many transitions are thought to occur both between neurons and within neurons.

A single mode of conduction
The multichannel model suggests there may exist nerve impulses which are, at present, completely undetectable. Impulses conveyed along lines of voltage sensors which are not coupled to the opening of ion channels will be characterized here as silent impulses, “stealth” impulses, or conformational impulses. Absent an action potential, they require an alternative power supply. At first glance this looks like something we don’t need — yet another mode of nerve conduction. In fact it points to a single molecular mechanism underlying and unifying all types of nerve conduction.

In this broader model, all communication down neurites, silent or detectable, depends upon functionally linked voltage sensors. By means of this molecular linkage, voltage sensor #2 is receiving an instruction (okay, go!) from its predecessor in the line, voltage sensor #1. This instruction carries the nerve impulse from sensor to sensor and from one end of the sensor array to the other.

To explore this broader definition of a nerve impulse suppose we start with the internode of a myelinated nerve. In this system we can observe an impulse that is detectable as an action potential at the node — becomes undetectable in its quick passage through the internode — and becomes detectable once again at the next node.

The nodes of Ranvier
There is an immediate hurdle for the multichannel nerve model presented in Chapter 2. It works readily enough for an unmyelinated nerve, but when you try to imagine how it might operate in a myelinated nerve, in saltatory conduction, the problem arises: If indeed we are looking at a multichannel neuron, then how could the identity and integrity of each channel be conserved when the signal jumps from node to node?

As a first step, let’s consider the possibility that transmission speed from node to node and within the node of a myelinated nerve can be varied. We want to see fast transmission between nodes and slow transmission at the node. There is an easy way to accomplish this within the model. Here is a single channel, one of 300.

The helix tightens at the nodes of Ranvier

If the channels are wrapped helically around the longitudinal axis of the neuron, then the impulse conduction speed is a function of the period of the helix. The longer the period, the faster the conduction of an impulse along the line of the nerve, and conversely.

This of course begs the question: Does a nerve impulse in passage actually duck under the myelin sheath, travel the length of the internode, and re-surface at the next node? Put another way, is saltatory conduction discontinuous — literally a jump — or is it continuous? Obviously I think it is a single continuous biochemical process from end to end. It is detectable only at the nodes because it manifests itself there electronically, with an influx of charged ions. In the internodes the impulse moves as a conformational wave which cannot be detected by electronic instruments. This is why the signal appears to hop from node to node.

The moving nerve impulse is preceded to the next node by an advance guard, a shift in transmembrane potential, just as in the conventional view of saltatory conduction. But the voltage shift’s effect on voltage sensors is slightly different — momentarily delayed, as we shall see.

Until the late 1980s it was thought and taught that there were no Na+ channels underneath the myelin sheath between the nodes of Ranvier. However, when the internodes were demyelinated with lysolecithin and studied with loose patch clamps, the sodium channels were found to be present after all (Shrager, 1987.) Although unit sodium channels are less densely packed on the internodal membrane than unit sodium channels at the nodes, they are actually more numerous in the internodes. This seems reasonable given the larger surface area of the axolemma in the internodes.

In the multichannel model the unit sodium channels are linked into longitudinal channels. The number of longitudinal channels (about 300) does not change along the length of the axon. Only the period of their helical winding changes from node to internode. One assumes the difference in period accounts for the high density of unit Na+ channels found in the node, and for the low density of unit Na+ channels found in the internode.

The Conformational Wavefront
In the sequestered environment beneath the myelin sheath the sodium channels have no access to sodium ions. In this setting, “impulse” cannot mean an action potential. There could still be, however, an impulse or advancing wavefront of conformational changes in the longitudinal channel, since the voltage sensors are still active and responsive to transmembrane voltage changes produced by action potentials at the node.

In the limit, where the helix is pulled straight as a string, the conformational impulse achieves its fastest possible speed between nodes. A straight line or a least a much straighter line establishes a short, fast channel path from node to node.

At the node, the much shorter period of the helix sharply slows the linear progress of the impulse, and it produces an action potential there because access to extracellular Na+ ions is restored. The short period helix and long running passage of the longitudinal channel through the node assures a very substantial local buildup of intracellular positive charges in the form of sodium ions.

How it works
Suppose we position ourselves to watch this process at one node of Ranvier. Let’s say a nerve impulse has just arrived. We know this because an action potential appears at this node. What happens next?

Exactly as in the conventional view of saltatory conduction, action potential firing at this initial node produces a positive shift in transmembrane potential that can be felt and (theoretically) measured at points all the way up the axon.

The voltage change induced by the initial action potential is transmitted instantly (at the speed of light though cytosol) and is “felt” by voltage sensors at least as far away as the next node.

At that distance, the potential shift is only about +20 mV. This is sufficient to trigger an action potential at the next node and in the textbook model, it does exactly that. The present model is different, however, in that the action potential is momentarily restrained from firing. We shall see why in a moment.

At all points along the internode, the potential shift produced by the initial action potential will be greater than +20 mV, and maximal at the node where the initial action potential has just fired. This instantaneous voltage change precedes and will power the signal that is about to be sent, at much lower speed, via linked unit sodium channels, from one node to the next node.

The signal will move as a wave of conformational change sustained by the successive movement of positively charged voltage sensors.

Voltage sensors of all the unit sodium channels located between the nodes will be energized – even though these thoroughly ignored channels have no access to sodium.

Here is an animation adopted from a University of Washington site which discusses voltage gated sodium channels. The animation shows, at a single unit sodium channel, the piston-like action of a voltage sensor in opening the gate to the passage of sodium ions. Bear in mind this is a simplification. In a real prokaryotic sodium channel, for example, there are four voltage sensors, arrayed like pistons around the pore. The pore opening is animated, not as the swing of a trap door hinge, but rather like the divergence, from a center, of four expertly pivoted chopsticks. The tips of the chopsticks effect the opening of the pore.

In this animation, the exterior of the cell is depicted as “up,” and the interior of the cell is “down.” The interior of the cell is normally negative relative to the outside of the cell. A positive charge injection at the node suddenly makes the interior of the axon less negative. The positively charged voltage sensor responds by shifting upward, that is, normal to the axolemma. In the model, the upshift of the voltage sensor is restrained — latched — until the voltage sensor of the preceding unit Na+ channel has popped up.

When the first action potential is fired at the initial node, one would expect to see all the voltage sensors at the next node, and in the intervening internode as well, react instantly. In this animation, the positively charged voltage sensor ascends suddenly and the sodium channel gate pops wide open.

For the multichannel model, however, the unselective activation of voltage sensors would create a huge problem, as noted in the opening paragraphs of this chapter. If transmembrane voltage change and reacting voltage sensors were the whole story, then the sodium ports of all 300 longitudinal channels would open simultaneously. The identity of a signal on any one longitudinal channel — i.e., its channel number — would be forever lost. Swamped out.

Na+ channels as a row of dominos.

To keep this from happening we must stipulate that no unit sodium channel may open until the preceding unit sodium channel has already opened. Put another way, the unit sodium channels, each with its array of voltage sensors, must open successively, like a row of falling dominos. This conserves the integrity of the individual numbered channels. It also prevents the spurious opening of the 299 longitudinal channels which are not, at the moment, conveying a signal.

It seems easiest to visualize the passage of the conformational wavefront as an unlatching process. Each and every voltage sensor is impelled to move by the elevated voltage gradient along the axon. But let’s assume that the movements of the voltage sensors are initially restrained, in every Na+ channel, by a latch.

There are several different ways to model the latching and unlatching (triggering) of the voltage sensor.

One I find promising is a conformational change affecting the vestibule of the gating canal. This canal is the protein “bearing” through which the voltage sensor freely slides.

Altering the depth of the vestibule changes the energetics of the voltage sensor: It can raise and lower energy barriers to the sensor’s movement — essentially without touching it. This might constitute a trigger or unlatching mechanism. See the work of Alexander Peyser et al.

This is a soft machine. One cannot expect to find ratchets and pawls. The equivalent is to be sought in energy barriers, wells and troughs. Changing the energetics of the system is not exclusively a problem in protein dynamics. Localized tension and sudden relaxation of the lipid membrane in and around the vestibule of the gating canals could unlatch a nearby sensor within a fourfold array of voltage sensors.

In a potassium channel four voltage sensors surround the pore. Each sensor moves independently. One sensor always rises first, but it is not clear if it is always the same one. The pore does not open until all four pistons have topped.

The sodium channel is similarly configured, but the pore opening is powered by just 3 of the 4 voltage sensors. The fourth voltage sensor lags behind the ascent of the first three by a number of milliseconds. When it does finally ascend, the fourth voltage sensor acts to close the pore and, thus, inactivates the sodium channel.

It could be that the fourth sensor somehow unhooks the pore from the winched home position achieved by the first three sensors — and the pore simply snaps shut.

In various types of ion channels, one could imagine an evolutionary pressure to roughly synchronize three or four voltage sensors. The presence of an underlying positive charge inside the cell is not necessarily a sufficient trigger. In a strongly bistable system, there can be an energy barrier that must be flattened or overcome before any sensor can ascend.

Within a single sodium channel, it is possible that the ascent of the first voltage sensor unlatchs, perhaps in rapid succession, the ascent of the remaining pair of pore-opening voltage sensors. If a successive unlatching mechanism operates within a single sodium channel, it is not much of a reach to imagine this same mechanism could be extended to the next neighboring sodium channel in a long line of sodium channels.

Deepening the vestibule can unlatch a voltage sensor. One could accomplish this by releasing tension normally applied to (steadily tugging upon) a molecular anchor in lipid, reshaping and deepening the vestibule.

To return to the internode model: Whatever the molecular device, to permit the movement of the voltage sensor a metaphoric latch must be pulled by the ascent of the preceding voltage sensor. Once released, the sensor rises like a slightly twisting piston. This may help open a sodium pore – a trivial gesture where there is no sodium – but far more importantly, it releases the latch on the next voltage sensor in line.

The conformational wavefront must unlatch unit sodium channels in sequential order, one right after the other, on its passage through the internode to the next node. It borrows its energy from the pre-cocked voltage sensors.

In the internode, under the myelin sheath, the sodium channels are not likely to actually open in the normal fashion, since there are no incoming Na+ ions. The channels are making, in effect, a dry run. This could be a molecular parody of the normal operation of the channel in an unmyelinated nerve. The motion of the sensor might also be uncoupled, in the internode, from the opening of the channel. This would speed up the impulse. In any event, because an impulse passes along a single specific numbered longitudinal channel as a conformational wavefront, the channel itself will perfectly conserve the identity (channel number) of this signal.

When the wavefront arrives at the node, sodium ions are once again available and the voltage gated doors open productively. Sodium ions pour into the cell and accumulate there as the impulse circles round and round, making a thorough job of it.

Note that as the conformational wavefront moves into the next internode, it will encounter the induced voltage gradient at its strongest. The voltage sensors will pop up like champagne corks. However, as the wavefront progresses along the axon, it also moves down the voltage gradient. Evolution will have set the length of the myelinated region so that it is just long enough to let the conformational wavefront reach the next node before it actually peters out.

Sodium channel structure
The molecular structure of a potassium channel was first solved by Roderick MacKinnon et al at Rockefeller, and published in 1998. MacKinnon was awarded the Nobel Prize in Chemistry for his work in 2003. But the eukaryotic sodium channel, a long and complicated monomer, has resisted analysis by x-ray crystallography.

Fortunately, surprisingly, in 2001 a voltage-gated sodium channel was discovered by Ren et al in bacteria. The prokaryotic sodium channels resemble potassium channels in that they are tetramers made up from four identical, relatively short proteins. Any of these short monomers can be successfully crystallized and analyzed. This made it possible, ultimately, to discern with crystallography the structure of a sodium channel. The first bacterial sodium channel structure to be fully worked out was published in Nature in July, 2011.

The crystal structure of a voltage-gated sodium channel
Jian Payandeh, Todd Scheuer, Ning Zheng & William A. Catterall
Nature 475, 353–358 (21 July 2011) doi:10.1038/nature10238

This work was done by Jian Payandeh at the University of Washington using a bacterial sodium channel. He is now at Genentech.

A few months later in December, 2011, an impressive analysis (and animation) of the voltage sensor’s moving parts was published in a PNAS paper, again from the University of Washington.
Structural basis for gating charge movement in the voltage sensor of a sodium channel
Vladimir Yarov-Yarovoy, Paul G. DeCaen, Ruth E. Westenbroek, Chien-Yuan Pan, Todd Scheuer, David Baker, and William A. Catterall

Na+ Channel concentration at nodes
The model of saltatory conduction we have been discussing here is consistent with the dense concentration of sodium channels observed at the nodes of Ranvier.

Photo courtesy of Bruce Willey, who shot it at the Skyline Slabs. In the molecular metaphor, the looped out sodium channels accumulate in the climber’s left hand, the “node”, as the rope gets shorter and shorter.

Since there is indeed a high concentration of sodium channels at the nodes, maybe this is a hint that the conduction channels from node to node have been tugged straight in the course of evolution and, in individuals, in the course of development.

A single mode of signaling
In the conventional model of saltatory conduction, the nerve is supposed to switch back and forth repeatedly between two distinct signaling modes: the action potential and passive conduction. In the model sketched here, there is a single mode of operation throughout. The voltage sensors of the unit sodium channels are displaced like a row of falling dominos from one end of the axon to the other. A wavefront of conformational change carries the signal the full length of a longitudinal channel, dry or wet. What changes between the node and the internode is the availability of extracellular Na+. It is possible that in the internode the channel opening is uncoupled from the voltage sensor, or that the channel opening is inactivated another way. But no matter what happens to the channels, the voltage sensors carry the signal in a continuous wave, beginning to end.

Stealth conduction:
Nerve impulses without action potentials
The concept of a conformational wavefront could prove helpful in modeling the dendrites, where information is able to move some distance without resorting to an action potential.

As noted above, in this model the nerve impulse is always carried by a line of voltage sensors. The impulse can be powered by an action potential, as it is on an unmyelinated axon. But an impulse can also move using voltage sensors alone, unencumbered by a fellow-traveling action potential. One might look for this “stealth” mode of transmission in the outer segments of photoreceptors and in other dendrites.

For a nerve impulse to move without relying on ion channels to produce an action potential, there must be an alternative power supply. Something other than an accompanying action potential must create a positive charge inside the neuron.

In a myelinated axon, the positive charge is created by a fixed point action potential, at the node, that is simply left behind when the moving impulse ducks under the myelin sheath and loses access to Na+ ions. Myelin insulation keeps the positive charge from degrading rapidly with distance from the sourcepoint. The positive transmembrane voltage shift can still be detected as far as 3 mm away at the next node.

In the outer segment of photoreceptors, the positive charge could be created by inverted sodium pumps in the rims of the disks. This would position a positive charge directly underneath the voltage sensors in the membrane. The Na+ ion channels could be inactivated. The line of voltage sensors, alone, can carry the impulse the length of the disk stack, using positively charged disk rims as an alternative power supply.

And in conventional types of dendrites? No one knows how dendrites work, but it would not be surprising to me if they do indeed use stealthy, undetectable impulses, hurrying from point to point along lines of voltage sensors. These signals would have to be using, as a powerplant, positive charges positioned beneath the voltage sensors by some means other than action potentials. Presumably, this would be the influx of Na⁺ and Ca⁺⁺ ions associated with the excitatory post synaptic potential (EPSP). Sub-membrane positive charges may be localized or concentrated beneath the sodium channels.

In addition to the ligand gated receptors that admit sodium and calcium ions through the post synaptic membrane, the dendrites are populated with voltage-gated sodium, calcium and potassium channels. Action potentials occasionally appear in the dendrites, so these channels are fairly numerous. The impulses are called dendritic spikes in this setting.

We can surmise that lines of linked voltage-sensors in the dendrites could silently accomplish a pass-through, to the axon, of signals received from numbered channels in the preceding neurons. In other words, the channel identities could be kept intact on their passage through the dendrites — much as they are kept intact on their way through the internodes. Signals in the dendrites conveyed by successively unlatching voltage sensors might bypass the hypothetical commutator and go straight to the multichannel axon.

If indeed there exists a commutator, the dendritic signals might manipulate or control the commutator selector in some way. In fact a ring or line of linked voltage sensors might be the commutator.

The linked channels could also be used to form calculational pathways. For example, to multiply by 2, an incoming signal on dendritic channel 2 stimulates an outbound (axon) channel 4.

How many of these stealth channels are there? Possibly in a range from hundreds to thousands of channels.

Must they fire one at a time? Can they fire five at a time? Is there a cumulative or “summation” effect and, therefore, an accumulator of some sort? How do the stealth channels converge to the axon hillock? Is there a dense structure in the membrane that could be detected or discerned where they converge?

Interestingly, in this model, the EPSP is not a signal: It is the signal’s power supply. The signal itself, carried by the successive unlatching of voltage sensors in an individual longitudinal channel — goes undetected. If we monitor the generalized, summed amplitudes of the EPSPs, we are monitoring in an approximate way the population count of active stealth channels. By the same line of reasoning, an IPSP will de-energize or un-cock the lines of voltage sensors. If the negative charge is sufficient, the voltage sensors will lose their ability to convey a stealth impulse.

How does the C. elegans nervous system work?
From its genome, it is clear that C. elegans does not have any voltage-gated sodium channels. This might make it an interesting system in which to pursue the problem of nerve impulses that can move without action potentials – as indeed its neurons do not use action potentials in the conventional sense.

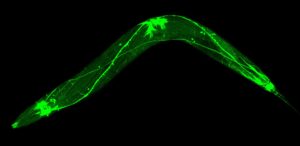The transparent worm’s miniature nervous system, which consists of just 302 neurons, is illuminated with green fluorescent protein.

The action potential exists to move nerve impulses for long distances on axons. In principle the distance over which an action potential can be sustained is almost unlimited. The recurrent laryngeal nerve axon of the giraffe is 15 feet long. The dorsal root ganglion of the blue whale is estimated to be 75 feet long.

But the C. elegans nervous system has evolved in the opposite direction. The worm is just 1 mm long, that is to say, the whole animal is about as long as the diameter of a giant squid axon. The diameters of C. elegans‘ nerve processes are just 100 to 200 nanometers. At diameters smaller than 500 nm, action potentials become erratic and unpredictable. Apparently the animal has successfully miniaturized its nervous system by eliminating action potentials altogether. Its 302 neurons do support signalling over tiny distances. But how, exactly?

We will hypothesize that the C. elegans neuron transmits signals using linked voltage sensors. Per the model, we would expect to find linked voltage sensors in any creature’s axon. But in the worm, the voltage sensors’ ability to produce an accompanying action potential does not exist. No sodium channels.

This is odd. Were the sodium channels never present? Or have ancient sodium channels been eradicated? If they were once present in ancestral neurons then does a network of sodium channel voltage sensors survive in C. elegans, perhaps along with vestigial, unlinked or otherwise permanently inactivated pores?

A first step might be check the worm’s big, 100 million base pair genome to see whether the entire gene for the sodium channel has been lost. If some sodium channel code does remain, as a kind of foreshortened pseudogene, then do these sequences encode voltage sensor domains that can still be expressed?

A solitary voltage sensor can function. Its operation does not depend on its typical association with an ion channel pore. For example, in the special case of a voltage sensor activated enzyme, a phosphatase, it has been shown the voltage sensor can readily work in isolation.

If there is no surviving network of sodium channel voltage sensors, then as a fallback, there are plentiful voltage sensors associated with potassium and calcium channels that are expressed in C. elegans. Perhaps calcium or potassium channels could supply the voltage sensors required (absolutely) by the model suggested here.

Although it has no sodium channels, C. elegans has 76 different varieties of potassium channels. Some are voltage gated, some are ligand gated.

Note that eukaryotic sodium and calcium channels are each continuous strands of protein encoded by single genes. In potassium channels, in contrast, there are four distinct but identical proteins that assemble into a tetramer. Each of the four discrete protein components includes one of the crucial S4 voltage sensor domains. Normally the K channel monomers assemble themselves into quads, but given the remarkable variety of K channels in the C. elegans genome, perhaps a variant — a long linear or looped, heterogeneous assemblage of monomers — is not out of the question.

It would be more conservative to suggest a silenced but conventional ion channel tetramer in which the sensors are active but the pore is unlinked, inactivated, truncated, or permanently closed. Also active, in this model, is the unlatching mechanism that links one ion channel to the next in line.

The linked voltage sensor concept may be able to account for the mysterious electronics of the C. elegans nervous system. Some and perhaps most of the worm’s nerves are able to meet the model’s requirement for a voltage shift as a power supply. The nerve has been found to function as a Schmitt trigger analog. The transmembrane voltage can assume two stable states or plateaus. From the model, one would immediately suggest that the voltage shift serves to “cock” or energize a line of linked voltage sensors.

In other words the Schmitt trigger is the powerplant. It is analogous to the EPSP in dendrites, to the inverted sodium pump in photoreceptor disks, and to the localized action potential firing at the nodes of Ranvier.